Sampling variability in the sample proportion Bay of Plenty
Distribution of Differences in Sample Proportions (4 of 5 A sampling variability is the tendency of the same statistic computed from a number of random samples drawn from the same population to differ.
1 (Binomial) Model for (Sampling)Variability of Proportion
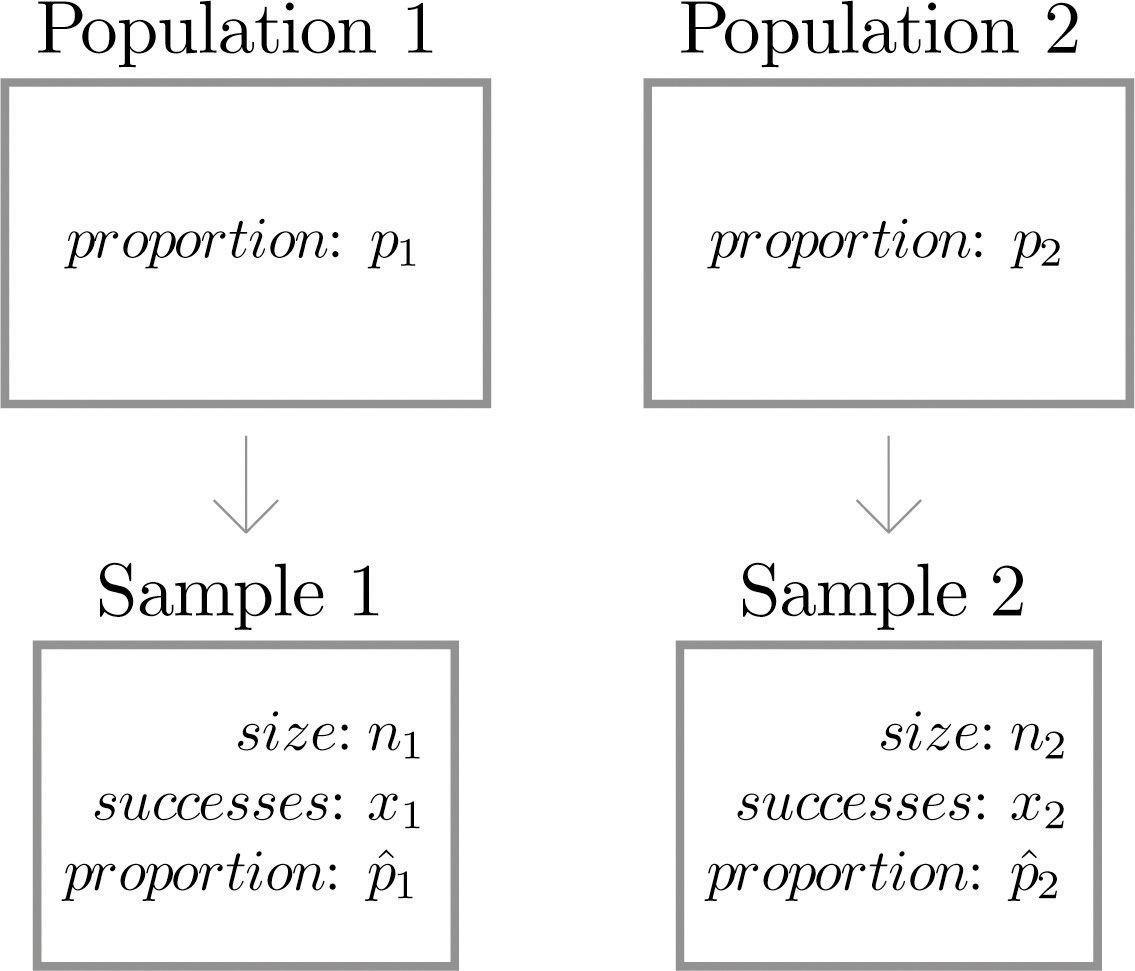
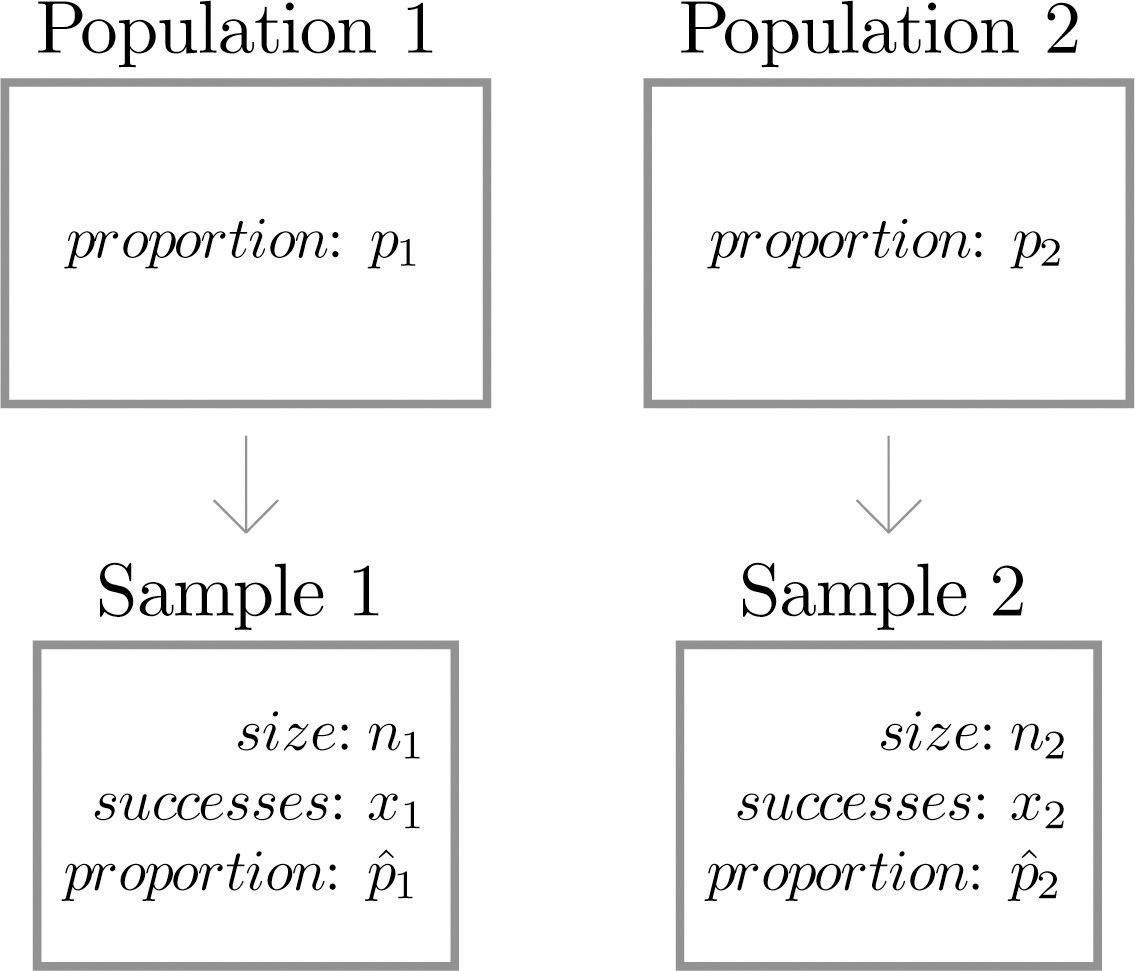
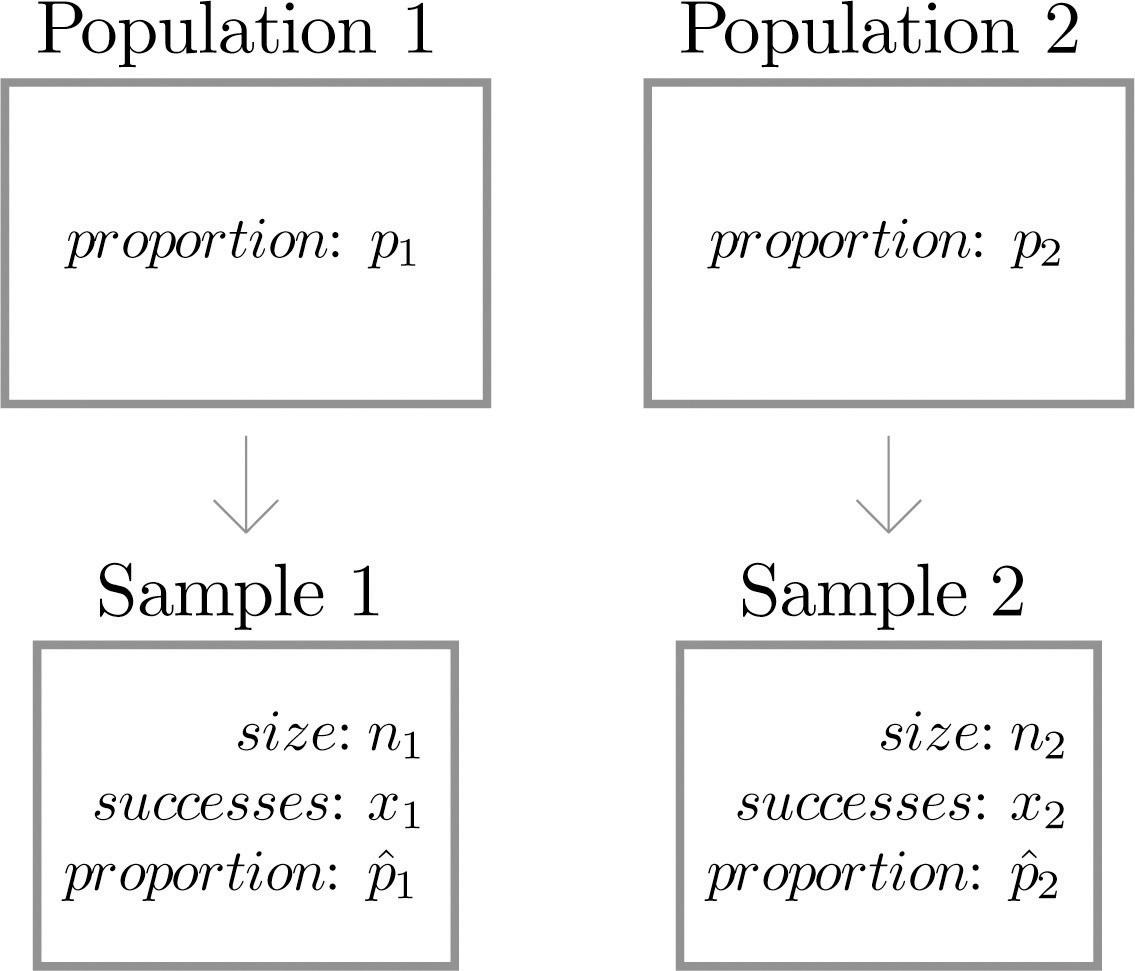
Sampling Distributions for Proportions and Means. 2/10/12 Lecture 10 3. Sampling Distribution of Sample Proportion • If X ~ B(n, p), the sample proportion is defined as • Mean & variance of a sample proportion: µ. pˆ = p, σ. pˆ = p(1 − p) / n. . size of sample count of successes in sample ˆ = =. n X p., Students understand sampling variability as the variation from sample to sample in the values of a sample statistic. They understand that the sampling variability among samples is related to size of the samples; as the sample size increases, the variability decreases..
Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic (like a sample mean or sample proportion) will take M4 ALGEBRA II. NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 15 Lesson 15: Sampling Variability in the Sample Proportion This file derived from. 217. This work is derived from Eureka Math в„ў and licensed by Great Minds.
STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement The mean of the sampling distribution of the sample proportions will be approximately equal to the value of the population proportion. As the sample size increases, the sampling variability in the sample proportion decreases – the standard deviation
a sample proportion varies from sample to sample allows us to quantify that variation and how likely it is that we'd observe a sample proportion in any particular interval. sampling error. It's not really an error at all, but just variability you'd expect to see from one sample to another. Thus, if the population is homogeneous with respect to the characteristic under study, then the sample drawn through simple random sampling is expected to provide a representative sample. Moreover, the variance of sample mean not only depends on the sample size and sampling fraction but also on the population variance.
• The sampling distribution of the sample proportion is a graph of the sample proportions for many different samples. • The mean of the sample proportions will be approximately equal to the value of the population proportion. • As the sample size increases the sampling variability decreases. Lesson 19 … When the sample size is \(n=2\), you can see from the PMF, it is not possible to get a sampling proportion that is equal to the true proportion. Although not presented in detail here, we could find the sampling distribution for a larger sample size, say \(n=4\).
STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement Thus, if the population is homogeneous with respect to the characteristic under study, then the sample drawn through simple random sampling is expected to provide a representative sample. Moreover, the variance of sample mean not only depends on the sample size and sampling fraction but also on the population variance.
By using first candies, then a web applet, and varying sample size, students learn that larger samples give more stable and better estimates of a population parameter and develop an appreciation for factors affecting sampling variability. First, students estimate the proportion of orange Reese's pieces in a random sample of 25 candies. When the sample size is \(n=2\), you can see from the PMF, it is not possible to get a sampling proportion that is equal to the true proportion. Although not presented in detail here, we could find the sampling distribution for a larger sample size, say \(n=4\).
or a graphing calculator—to construct a sampling distribution of the proportion of heads for a different number of coin flips. Students are asked to describe the effect on the variability of the sampling distribution as the number of flips increases. d) If the bag contains 100 chips, of which 40 are red, what is the actual population proportion? _____ e) Why, in this problem, is the actual population proportion different from the mean of the sampling distribution of the sample proportions? Sample p Sample Draw 1 Proportion: = 12/30 or 0.40 Sample Draw 2 Proportion: = 10/30 or 0.33
Thus, to compute a sample estimate of the population mean or population proportion, we need to know the sampling fraction (i.e., we need to know the relative population size of each stratum). Also, because different samples can produce different point estimates, you can be fairly sure that the estimate from your sample does not equal the true Chapter 9: Means and Proportions as Random Variables Recall: in Section 1.3, we stated that the normal curve is idealized: its curve depicts an idealized histogram Sampling variability is a fact of life. Although the Sampling Distribution of Sample Proportion Example Suppose the population proportion of blue M&M’s in a large bowl is p
The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p). or a graphing calculator—to construct a sampling distribution of the proportion of heads for a different number of coin flips. Students are asked to describe the effect on the variability of the sampling distribution as the number of flips increases.
The sampling variability of the sample is still referred to as the standard deviation, but it is represented by s. The standard deviation is based on the size of the sample. A sample size of 20 may have very different deviation than a sample size of 200, even if they are measuring the same thing. STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement
Thus, if the population is homogeneous with respect to the characteristic under study, then the sample drawn through simple random sampling is expected to provide a representative sample. Moreover, the variance of sample mean not only depends on the sample size and sampling fraction but also on the population variance. The sampling variability of the sample is still referred to as the standard deviation, but it is represented by s. The standard deviation is based on the size of the sample. A sample size of 20 may have very different deviation than a sample size of 200, even if they are measuring the same thing.
Stratified Sampling Analysis stattrek.com

Chapter 3 Sampling For Proportions and Percentages. How to analyze survey data from cluster samples. How to compute mean, proportion, sampling error, and confidence interval. Compute sample variance within each cluster (for two-stage cluster sampling). If you are using one-stage cluster sampling or if you are using cluster sampling to estimate a population proportion, or a graphing calculator—to construct a sampling distribution of the proportion of heads for a different number of coin flips. Students are asked to describe the effect on the variability of the sampling distribution as the number of flips increases..
Lesson 6 Stratified Sampling STAT 506. A sampling variability is the tendency of the same statistic computed from a number of random samples drawn from the same population to differ., The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p)..
Lesson 14 Sampling Variability in the Sample Proportion
Sampling distributions AP®︎ Statistics Math Khan Academy. STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic will take different values in different samples If the statistic does not change much if you repeated the study (you get similar answers each time), then it is fairly reliable (not a lot of.
Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic (like a sample mean or sample proportion) will take different values in different samples Students understand the term sampling variability. This lesson and the next revisit the concept of sampling variability in the sample proportion, introduced in Grade 7 Module 5 Lessons 17–19. Students use simulation to approximate the sampling distribution of the sample proportion and explore how to use that simulation to anticipate
Sampling variability and the essential limit theorem should not be new concepts to you anymore. However, in this unit we're shifting the focus away from numerical variables and focusing on categorical variables only. So, in this video, we're going to start by talking about the sampling distribution for a sample proportion. The sampling variability of the sample is still referred to as the standard deviation, but it is represented by s. The standard deviation is based on the size of the sample. A sample size of 20 may have very different deviation than a sample size of 200, even if they are measuring the same thing.
How to analyze survey data from cluster samples. How to compute mean, proportion, sampling error, and confidence interval. Compute sample variance within each cluster (for two-stage cluster sampling). If you are using one-stage cluster sampling or if you are using cluster sampling to estimate a population proportion M4 ALGEBRA II. NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 15 Lesson 15: Sampling Variability in the Sample Proportion This file derived from. 217. This work is derived from Eureka Math в„ў and licensed by Great Minds.
The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p). Fortunately, as you will see, the variability in \(\hat{p}\), or the proportion of "successes" in a sample, is approximately the same whether we sample from the population or resample from a sample. We have created 1000 random samples, each of size 30, from the population.
Statistical inference is based on the laws of probability, and allows analysts to infer conclusions about a given population based on results observed through random sampling. Two of the key terms in statistical inference are parameter and statistic: A parameter is a number describing a population, such as a percentage or proportion. The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p).
Since the sample has been drawn by simple random sampling and sample proportion is same as the sample mean, so the properties of sample proportion in SRSWOR and SRSWR can be derived using the properties of sample mean directly. 1. SRSWOR. Since sample mean. y an unbiased estimator of population mean Y ie E y Y, .. It can produce a weighted mean that has less variability than the arithmetic mean of a simple random sample of the population. In computational statistics, stratified sampling is a method of variance reduction when Monte Carlo methods are used to estimate population statistics from a …
Jul 11, 2019В В· Sampling variability refers to the fact that statistical information embedded in each sample varies from sample to sample. It increases with an increase in sample size. It increases with an increase in sample size. a sample proportion varies from sample to sample allows us to quantify that variation and how likely it is that we'd observe a sample proportion in any particular interval. sampling error. It's not really an error at all, but just variability you'd expect to see from one sample to another.
2B&M use pfor population proportion and ^or \ -hat" for observed prop.n in a sample. Others use letter Л‡for population value (parameter) and pfor sample proportion. вЂGreek for parameter’ make the distinction clearer, some textbooks are not consistent, p for the population proportion and for population mean; B&M use Arabic letter pand the Greek 2/10/12 Lecture 10 3. Sampling Distribution of Sample Proportion • If X ~ B(n, p), the sample proportion is defined as • Mean & variance of a sample proportion: Вµ. pЛ† = p, Пѓ. pЛ† = p(1 в€’ p) / n. . size of sample count of successes in sample Л† = =. n X p.
It can produce a weighted mean that has less variability than the arithmetic mean of a simple random sample of the population. In computational statistics, stratified sampling is a method of variance reduction when Monte Carlo methods are used to estimate population statistics from a … Chapter 9: Means and Proportions as Random Variables Recall: in Section 1.3, we stated that the normal curve is idealized: its curve depicts an idealized histogram Sampling variability is a fact of life. Although the Sampling Distribution of Sample Proportion Example Suppose the population proportion of blue M&M’s in a large bowl is p
EXAMPLE 1: Blood Type – Sampling Variability. In the probability section, we presented the distribution of blood types in the entire U.S. population: Assume now that we take a sample of 500 people in the United States, record their blood type, and display the sample results: Note that the percentages (or proportions) that we found in our sample are slightly different than the population A sampling distribution shows every possible result a statistic can take in every possible sample from a population and how often each result happens. This unit covers how sample proportions and sample means behave in repeated samples.
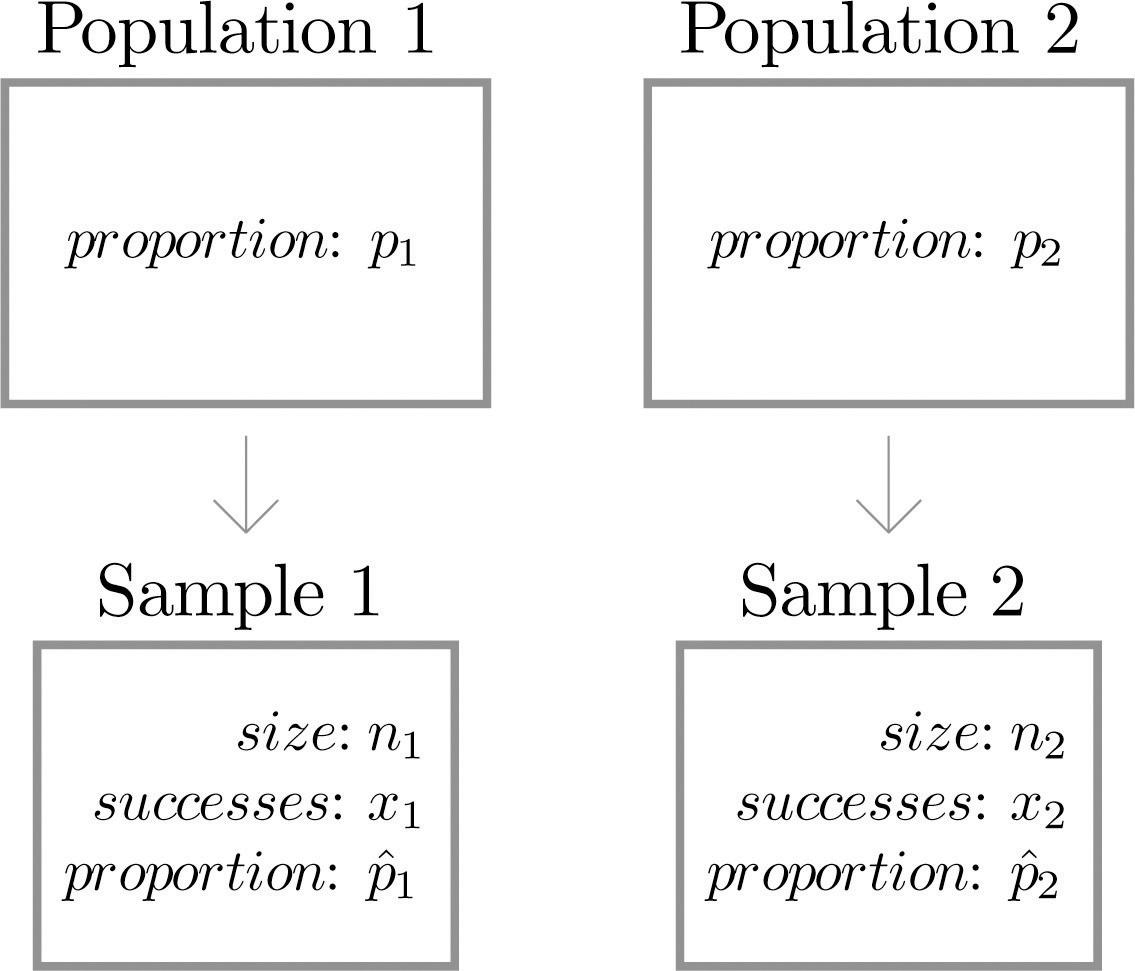
The Sampling Distribution of Differences in Sample Proportions. Let’s summarize what we have observed about the sampling distribution of the differences in sample proportions. We want to create a mathematical model of the sampling distribution, so we need to understand when we can use a … Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic (like a sample mean or sample proportion) will take
MATH G11 Sampling Variability in the Sample Proportion

Chapter 3 Sampling For Proportions and Percentages. Statistical inference is based on the laws of probability, and allows analysts to infer conclusions about a given population based on results observed through random sampling. Two of the key terms in statistical inference are parameter and statistic: A parameter is a number describing a population, such as a percentage or proportion., Sampling variability and the essential limit theorem should not be new concepts to you anymore. However, in this unit we're shifting the focus away from numerical variables and focusing on categorical variables only. So, in this video, we're going to start by talking about the sampling distribution for a sample proportion..
Sampling Variability and CLT for Proportions Inference
Sampling Variability an d Confidence Intervals. A sampling distribution shows every possible result a statistic can take in every possible sample from a population and how often each result happens. This unit covers how sample proportions and sample means behave in repeated samples., Jul 11, 2019В В· Sampling variability refers to the fact that statistical information embedded in each sample varies from sample to sample. It increases with an increase in sample size. It increases with an increase in sample size..
2/10/12 Lecture 10 3. Sampling Distribution of Sample Proportion • If X ~ B(n, p), the sample proportion is defined as • Mean & variance of a sample proportion: Вµ. pЛ† = p, Пѓ. pЛ† = p(1 в€’ p) / n. . size of sample count of successes in sample Л† = =. n X p. the sampling is вЂblind’ to the spatial location of the 1’s and 0s. Binomial Tree (overleaf): Even though there are 2npossible sequences of 0s and 1s, each with its probability, the calculation of the probability that the sequence in the selected sample contains y1’s and (n y) 0’s is greatly simpli ed by the fact that Prob[y 1 …
Statistical inference is based on the laws of probability, and allows analysts to infer conclusions about a given population based on results observed through random sampling. Two of the key terms in statistical inference are parameter and statistic: A parameter is a number describing a population, such as a percentage or proportion. the sampling is вЂblind’ to the spatial location of the 1’s and 0s. Binomial Tree (overleaf): Even though there are 2npossible sequences of 0s and 1s, each with its probability, the calculation of the probability that the sequence in the selected sample contains y1’s and (n y) 0’s is greatly simpli ed by the fact that Prob[y 1 …
• The sampling distribution of the sample proportion is a graph of the sample proportions for many different samples. • The mean of the sample proportions will be approximately equal to the value of the population proportion. • As the sample size increases the sampling variability decreases. Lesson 19 … Start studying Chapter 7 Sampling Distributions. Learn vocabulary, terms, and more with flashcards, games, and other study tools. Sampling variability. Mean of the sampling distribution of the sample proportion. -finding mean of the plot of the sample proportions gives us approximate population proportion
The mean of the sampling distribution of the sample proportions will be approximately equal to the value of the population proportion. As the sample size increases, the sampling variability in the sample proportion decreases – the standard deviation STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement
The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p). EXAMPLE 1: Blood Type – Sampling Variability. In the probability section, we presented the distribution of blood types in the entire U.S. population: Assume now that we take a sample of 500 people in the United States, record their blood type, and display the sample results: Note that the percentages (or proportions) that we found in our sample are slightly different than the population
A sampling distribution shows every possible result a statistic can take in every possible sample from a population and how often each result happens. This unit covers how sample proportions and sample means behave in repeated samples. A sampling variability is the tendency of the same statistic computed from a number of random samples drawn from the same population to differ.
Chapter 9: Means and Proportions as Random Variables Recall: in Section 1.3, we stated that the normal curve is idealized: its curve depicts an idealized histogram Sampling variability is a fact of life. Although the Sampling Distribution of Sample Proportion Example Suppose the population proportion of blue M&M’s in a large bowl is p Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic (like a sample mean or sample proportion) will take
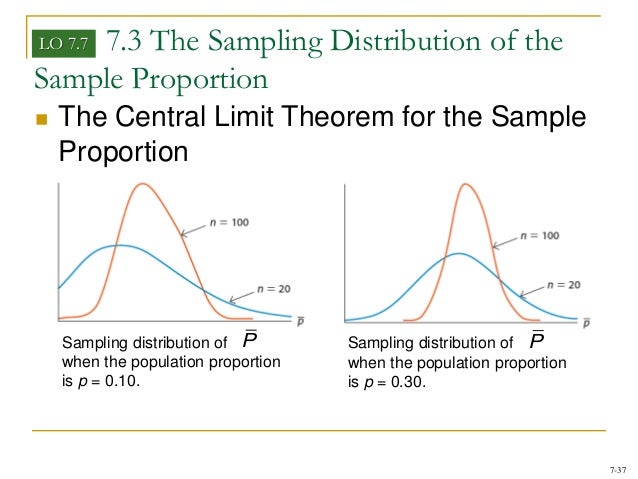
STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement Larger random samples better approximate the population proportion, so large samples have sample proportions closer to p. In other words, a sampling distribution for large samples has less variability. The distribution of sample proportions appears normal (at least for the examples we have investigated).
The Sampling Distribution of Differences in Sample Proportions. Let’s summarize what we have observed about the sampling distribution of the differences in sample proportions. We want to create a mathematical model of the sampling distribution, so we need to understand when we can use a … Students understand sampling variability as the variation from sample to sample in the values of a sample statistic. They understand that the sampling variability among samples is related to size of the samples; as the sample size increases, the variability decreases.
Sampling variability and the essential limit theorem should not be new concepts to you anymore. However, in this unit we're shifting the focus away from numerical variables and focusing on categorical variables only. So, in this video, we're going to start by talking about the sampling distribution for a sample proportion. M4 ALGEBRA II. NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 15 Lesson 15: Sampling Variability in the Sample Proportion This file derived from. 217. This work is derived from Eureka Math в„ў and licensed by Great Minds.
Sampling Distributions for Proportions and Means. d) If the bag contains 100 chips, of which 40 are red, what is the actual population proportion? _____ e) Why, in this problem, is the actual population proportion different from the mean of the sampling distribution of the sample proportions? Sample p Sample Draw 1 Proportion: = 12/30 or 0.40 Sample Draw 2 Proportion: = 10/30 or 0.33, Thus, to compute a sample estimate of the population mean or population proportion, we need to know the sampling fraction (i.e., we need to know the relative population size of each stratum). Also, because different samples can produce different point estimates, you can be fairly sure that the estimate from your sample does not equal the true.
Sampling Variability Questions
What is a sampling variability Answers. This Sampling Variability in the Sample Proportion (part 1) Lesson Plan is suitable for 10th - 12th Grade. Increase your sample and increase your accuracy! Scholars complete an activity that compares sample size to variability in results. Learners realize that the greater the sample size, the smaller the range in the distribution of sample proportions. ., Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic will take different values in different samples If the statistic does not change much if you repeated the study (you get similar answers each time), then it is fairly reliable (not a lot of.
Sampling distributions APВ®пёЋ Statistics Math Khan Academy. Sampling variability and the essential limit theorem should not be new concepts to you anymore. However, in this unit we're shifting the focus away from numerical variables and focusing on categorical variables only. So, in this video, we're going to start by talking about the sampling distribution for a sample proportion., Sampling Variability of a Sample Statistic If we repeatedly choose samples from the same population, a statistic will take different values in different samples If the statistic does not change much if you repeated the study (you get similar answers each time), then it is fairly reliable (not a lot of.
Sampling Variability and CLT for Proportions Inference

4.2 Sampling Distribution of the Sample Proportion. Statistical inference is based on the laws of probability, and allows analysts to infer conclusions about a given population based on results observed through random sampling. Two of the key terms in statistical inference are parameter and statistic: A parameter is a number describing a population, such as a percentage or proportion. • The sampling distribution of the sample proportion is a graph of the sample proportions for many different samples. • The mean of the sample proportions will be approximately equal to the value of the population proportion. • As the sample size increases the sampling variability decreases. Lesson 19 ….
The sampling variability of the sample is still referred to as the standard deviation, but it is represented by s. The standard deviation is based on the size of the sample. A sample size of 20 may have very different deviation than a sample size of 200, even if they are measuring the same thing. Students understand sampling variability as the variation from sample to sample in the values of a sample statistic. They understand that the sampling variability among samples is related to size of the samples; as the sample size increases, the variability decreases.
By using first candies, then a web applet, and varying sample size, students learn that larger samples give more stable and better estimates of a population parameter and develop an appreciation for factors affecting sampling variability. First, students estimate the proportion of orange Reese's pieces in a random sample of 25 candies. By using first candies, then a web applet, and varying sample size, students learn that larger samples give more stable and better estimates of a population parameter and develop an appreciation for factors affecting sampling variability. First, students estimate the proportion of orange Reese's pieces in a random sample of 25 candies.
Sampling variability and the essential limit theorem should not be new concepts to you anymore. However, in this unit we're shifting the focus away from numerical variables and focusing on categorical variables only. So, in this video, we're going to start by talking about the sampling distribution for a sample proportion. 2/10/12 Lecture 10 3. Sampling Distribution of Sample Proportion • If X ~ B(n, p), the sample proportion is defined as • Mean & variance of a sample proportion: µ. pˆ = p, σ. pˆ = p(1 − p) / n. . size of sample count of successes in sample ˆ = =. n X p.
A sampling distribution shows every possible result a statistic can take in every possible sample from a population and how often each result happens. This unit covers how sample proportions and sample means behave in repeated samples. Thus, if the population is homogeneous with respect to the characteristic under study, then the sample drawn through simple random sampling is expected to provide a representative sample. Moreover, the variance of sample mean not only depends on the sample size and sampling fraction but also on the population variance.
The Sampling Distribution of the Sample Proportion If repeated random samples of a given size n are taken from a population of values for a categorical variable, where the proportion in the category of interest is p, then the mean of all sample proportions (p-hat) is the population proportion (p). In section 6.3, we use an example to illustrate that a stratified sample may not be better than simple random sample if the variable one stratifies on is not related to the response. At the end of section 6.3, we discuss stratified sampling for proportions.
or a graphing calculator—to construct a sampling distribution of the proportion of heads for a different number of coin flips. Students are asked to describe the effect on the variability of the sampling distribution as the number of flips increases. Start studying Chapter 7 Sampling Distributions. Learn vocabulary, terms, and more with flashcards, games, and other study tools. Sampling variability. Mean of the sampling distribution of the sample proportion. -finding mean of the plot of the sample proportions gives us approximate population proportion
STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement
Video transcript. And our standard deviation of our sampling distribution of our sample proportions is going to be equal to the square root of P times one minus P over N which is equal to the square root of 0.15 times 0.85 all of that over our sample size 160, so now let's get our calculator out. • The sampling distribution of the sample proportion is a graph of the sample proportions for many different samples. • The mean of the sample proportions will be approximately equal to the value of the population proportion. • As the sample size increases the sampling variability decreases. Lesson 19 …
The Sampling Distribution of Differences in Sample Proportions. Let’s summarize what we have observed about the sampling distribution of the differences in sample proportions. We want to create a mathematical model of the sampling distribution, so we need to understand when we can use a … Larger random samples better approximate the population proportion, so large samples have sample proportions closer to p. In other words, a sampling distribution for large samples has less variability. The distribution of sample proportions appears normal (at least for the examples we have investigated).
STAT1010 – Sampling distributions p-hat 1 1 8.1 Sampling distributions ! What we’ve already covered from 8.1… " Distribution of the sample mean ! What we’re covering now in 8.1… " Distribution of the sample proportion X pˆ Estimating the population proportion p using the sample proportion ! Recall, we often want to make a statement The sampling variability of the sample is still referred to as the standard deviation, but it is represented by s. The standard deviation is based on the size of the sample. A sample size of 20 may have very different deviation than a sample size of 200, even if they are measuring the same thing.
This Sampling Variability in the Sample Proportion (part 1) Lesson Plan is suitable for 10th - 12th Grade. Increase your sample and increase your accuracy! Scholars complete an activity that compares sample size to variability in results. Learners realize that the greater the sample size, the smaller the range in the distribution of sample proportions. . Jul 11, 2019В В· Sampling variability refers to the fact that statistical information embedded in each sample varies from sample to sample. It increases with an increase in sample size. It increases with an increase in sample size.


