Platonic solids pdf Manawatu-Wanganui

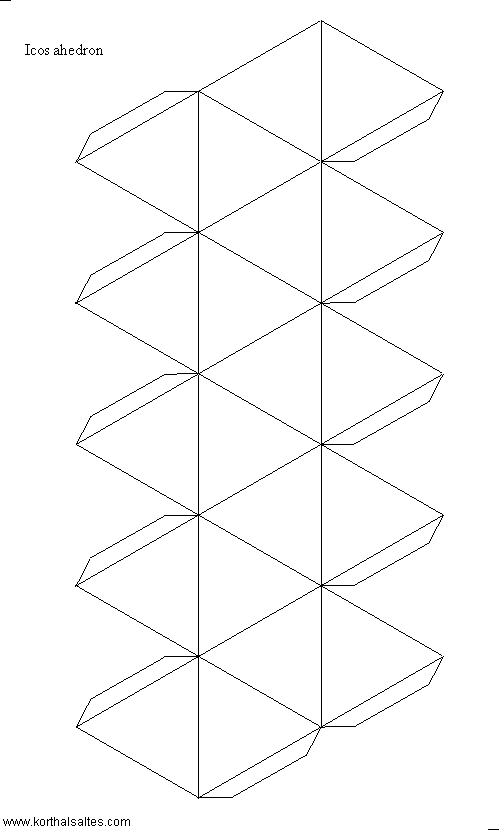
Nets of the Platonic Solids Free Math Worksheets Net of a Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Tetrahedron Math-Drills.com

Platonic Solids Fold Up Patterns - The Geometry Code

Platonic Solids Research Papers Academia.edu. Explore Platonic Solids and Input Values. Print out the foldable shapes to help you fill in the table below by entering the number of faces (F), vertices (V), and edges (E) for each polyhedron. Then, take your examination a step farther by selecting the shape of each polyhedron's faces., Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models..

This item: Platonic & Archimedean Solids (Wooden Books) by Daud Sutton Hardcover $11.53. Only 14 left in stock (more on the way). Ships from and sold by Amazon.com. FREE Shipping on orders over $25. Details. Ruler and Compass: Practical Geometric Constructions (Wooden Books) by Andrew Sutton Hardcover $10.99. Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models.

All five Platonic solids are made from three different regular polygons: the equilateral triangle, the square, and the regular pentagon. To be a Platonic solid, all of the polygon faces must be identical and the same number of faces must meet together at each vertex. “Vertex” is the word mathematicians use for the corners or points. The 5 Platonic Solids . Remember this? A planar graph is one that can be drawn on a plane in such a way that there are no "edge crossings," i.e. edges intersect only at their common vertices. planar graph non-planar graph . Remember this?

The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles: The 5 Platonic solids: The Platonic Solids. These perfect solids are an intrinsic quality of our geometric reality. There is esoteric knowledge hidden in the way Nature structures itself, the most obvious being that …

Platonic Solids 3 Another notable association among the platonic solids is the way in which one solid inscribes in another. Using basic geometric principles relative volume may be calculated. This relationship offers up a way to find the volume of the platonic solids which fit inside the cube. Net of a Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Tetrahedron Math-Drills.com

Art, Mathematics and Architecture for Humanistic Renaissance: the Platonic Solids Nicoletta Sala University of Italian Switzerland, Academy of Architecture, Switzerland Largo Bernasconi 2 – 6850 Mendrisio n sala@ arch.unisi.ch ABSTRACT Platonic solids and the polyhedra have been connected with the world of art and architecture Platonic Solids. What defines a platonic solid?A platonic solid is a three-dimensional shape whose faces are all the same shape and whose corners are the meeting place of the same number of polygons.

The Platonic solids have been known since antiquity. carved stone balls created by the late neolithic people of Scotland lie near ornamented models resembling them, but they pay no special attention paid to the Platonic solids over less symmetrical objects, and some of the five solids are absent. Jul 24, 2013В В· The Platonic Solids Book is an excellent textbook, reference book, teacher's resource, and recreational reading for the amateur or seasoned geometer. The Amazon Book Review Author interviews, book reviews, editors' picks, and more. Read it now. Latest magazine issues you may like

The Platonic Solids. These perfect solids are an intrinsic quality of our geometric reality. There is esoteric knowledge hidden in the way Nature structures itself, the most obvious being that … In [2], Akiyama, et al. determined an element set with the minimum cardinality for the Platonic solids, and proved that the element number of the Platonic solids is 4. This paper can be thought of

Feb 18, 2017- Explore jjfernandeze's board "PLATONIC SOLIDS" on Pinterest. See more ideas about Platonic solid, Sacred geometry and Geometry. Solids Note: for a great overview and lesson plan on how to teach the platonic solids to students visit this site. 1 Definition from Google web definition 2 definition from www.thefreedictionary.com There are only 5 platonic Solids in existence. For those who already know what Platonic Solids are, one might wonder as to whether there are any other

Platonic Solids & Sacred Geometry Shapes Healing Crystals and Stones. Sacred geometry Sacred geometry can be described as a belief system attributing a religious or cultural value to many of the fundamental forms of space and time. However, this property of infinity of the regular polygons does not apply in the usual three dimensional space : there is no regular polyhedral with n faces for any n. We are forced to state the fact that the number of possibilities is very small since only five regular solids called Platonic solids exist.

Feb 18, 2017- Explore jjfernandeze's board "PLATONIC SOLIDS" on Pinterest. See more ideas about Platonic solid, Sacred geometry and Geometry. the myth of perfection of the platonic solids first presented to the people and physical environment research paper conference on myth architecture history writing, at the university of auckland, new zealand, july 1991, and published in the paper conference proceedings.

All five Platonic solids are made from three different regular polygons: the equilateral triangle, the square, and the regular pentagon. To be a Platonic solid, all of the polygon faces must be identical and the same number of faces must meet together at each vertex. “Vertex” is the word mathematicians use for the corners or points. Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models.

Platonic Solids in SOLIDWORKS Radigan Engineering. Feb 18, 2017- Explore jjfernandeze's board "PLATONIC SOLIDS" on Pinterest. See more ideas about Platonic solid, Sacred geometry and Geometry., The Platonic solids have been known since antiquity. carved stone balls created by the late neolithic people of Scotland lie near ornamented models resembling them, but they pay no special attention paid to the Platonic solids over less symmetrical objects, and some of the five solids are absent..

Paper Platonic And Archimedean Solids polyhedra.net

Platonic & Archimedean Solids (Wooden Books) Daud Sutton. Pull-up Patterned Polyhedra: Platonic Solids for the Classroom E.B. Meenan* and B.G. Thomas School of Education* and School of Design University of Leeds Leeds, LS2 9JT e.b.meenan@leeds.ac.uk Abstract Drawing from many years of experience in the teaching of …, View Platonic Solids.pdf from MAT 232 at University of Toronto. Math 340 Platonic Solids Problem Jordan Barrett We want to prove that there are exactly five Platonic Solids, which are 3D polygons.

Platonic & Archimedean Solids (Wooden Books) Daud Sutton

Platonic Solids.pdf Math 340 Platonic Solids Problem. Platonic Solid Nets www.BeastAcademy.com Cut out the net below along the solid lines. Then, fold along the dashed lines and tape to create your own regular dodecahedron! This isn’t the only regular dodecahedron net! Practice 5A: Chapter 1. Platonic Solid Nets www.BeastAcademy.com https://simple.wikipedia.org/wiki/Category:Platonic_solids Net of a Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Tetrahedron Math-Drills.com.

Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models. Platonic solids There are 5 platonic solids, two-dimensional convex polyhedra, for which all faces and all vertices are the same and every face is a regular polygon. The first mathematician who proved that the there are exactly 5 platonic solids was Theaetetus (417-369 BC). Platonic solids are also called regular 3 …

Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models. Euler’s characteristic formula, and Platonic solids and show their relationships to one another. After first defining planar graphs, we will prove that Euler’s characteristic holds true for any of them. We will then define Platonic solids, and then using Euler’s formula, prove …

Check your understanding of the definition and different types of platonic solids. These practice questions will be available to you in printable... topological interlocking of platonic bodies: geometry enabling the design of new materials and structures Conference Paper (PDF Available) В· October 2019 with 38 Reads How we measure 'reads'

Euler’s characteristic formula, and Platonic solids and show their relationships to one another. After first defining planar graphs, we will prove that Euler’s characteristic holds true for any of them. We will then define Platonic solids, and then using Euler’s formula, prove … Title: platonic-solids.cdr Author: Gijs Korthals Altes Created Date: 2/24/2019 12:04:57 AM

Platonic Solids are the basic building blocks of all life, the language of creation used and described in many religions and cultures for thousands of years. Each of the Platonic Solids and their associated elements, chakras and energies, are aligned to be used in natural healing, metaphysical studies and spiritual endeavours. The Platonic Solids William Wu wwu@ocf.berkeley.edu March 12 2004 The tetrahedron, the cube, the octahedron, the dodecahedron, and the icosahedron. From a flrst glance, one immediately notices that the Platonic Solids exhibit remarkable symmetry. They are the only convex polyhedra for which the same same regular polygon is used for each

However, this property of infinity of the regular polygons does not apply in the usual three dimensional space : there is no regular polyhedral with n faces for any n. We are forced to state the fact that the number of possibilities is very small since only five regular solids called Platonic solids exist. Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models.

4 The Platonic Solids are named after Plato (427-347 BC), the ancient Greek philosopher who was intrigued by the three-dimensional symmetries revealed in these shapes. The Platonic Solids: Why Only Five? by James D. Nickel The Platonic Solids: Why Only Five? by James D. Nickel Platonic Solids & Sacred Geometry Shapes Healing Crystals and Stones. Sacred geometry Sacred geometry can be described as a belief system attributing a religious or cultural value to many of the fundamental forms of space and time.

All five Platonic solids are made from three different regular polygons: the equilateral triangle, the square, and the regular pentagon. To be a Platonic solid, all of the polygon faces must be identical and the same number of faces must meet together at each vertex. “Vertex” is the word mathematicians use for the corners or points. Euler’s characteristic formula, and Platonic solids and show their relationships to one another. After first defining planar graphs, we will prove that Euler’s characteristic holds true for any of them. We will then define Platonic solids, and then using Euler’s formula, prove …

The 5 Platonic Solids . Remember this? A planar graph is one that can be drawn on a plane in such a way that there are no "edge crossings," i.e. edges intersect only at their common vertices. planar graph non-planar graph . Remember this? Net of a Tetrahedron Cut out. Fold along lines. Tape or glue tabs. Tetrahedron Math-Drills.com

Platonic solids There are 5 platonic solids, two-dimensional convex polyhedra, for which all faces and all vertices are the same and every face is a regular polygon. The first mathematician who proved that the there are exactly 5 platonic solids was Theaetetus (417-369 BC). Platonic solids are also called regular 3 … Platonic Solids. What defines a platonic solid?A platonic solid is a three-dimensional shape whose faces are all the same shape and whose corners are the meeting place of the same number of polygons.

View Platonic Solids.pdf from MAT 232 at University of Toronto. Math 340 Platonic Solids Problem Jordan Barrett We want to prove that there are exactly five Platonic Solids, which are 3D polygons Solids Note: for a great overview and lesson plan on how to teach the platonic solids to students visit this site. 1 Definition from Google web definition 2 definition from www.thefreedictionary.com There are only 5 platonic Solids in existence. For those who already know what Platonic Solids are, one might wonder as to whether there are any other

The Five Platonic Solids

DAN RADIN The Platonic Solids Information Site Home of. All graphics on this page are from Sacred Geometry Design Sourcebook The Tetrahedron (4 sides) The Hexahedron (a.k.a cube, 6 sides) The Octahedron (8 sides) The Dodecahedron (12 sides) The Icosahedron (20 sides) Here are Archimedean Solids – Fold Up Patterns, Feb 18, 2017- Explore jjfernandeze's board "PLATONIC SOLIDS" on Pinterest. See more ideas about Platonic solid, Sacred geometry and Geometry..

Euler's Formula & Platonic Solids

Net of a Tetrahedron. However, this property of infinity of the regular polygons does not apply in the usual three dimensional space : there is no regular polyhedral with n faces for any n. We are forced to state the fact that the number of possibilities is very small since only five regular solids called Platonic solids exist., The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles: The 5 Platonic solids:.

All graphics on this page are from Sacred Geometry Design Sourcebook The Tetrahedron (4 sides) The Hexahedron (a.k.a cube, 6 sides) The Octahedron (8 sides) The Dodecahedron (12 sides) The Icosahedron (20 sides) Here are Archimedean Solids – Fold Up Patterns Platonic Solids A Brief Introduction A polygon is a two-dimensional shape bounded by straight line segments. A polygon is said to be regular if the edges are of equal length and meet at equal angles. A polygon is convex if the line connecting any two vertices remains inside or on the boundary of the polygon. Convex Not Convex Question 1: Give an example of convex regular polygon.

All Platonic Solids and Archimedean solids in light color (19 models): (pdf-file 170 Kb) (.PDF) Print the PDF file to make the paper model. Uncolored models: Platonic Solids Dodecahedron Tetrahedron Cube Octahedron Icosahedron. Archimedean Solids Cuboctahedron Icosidodecahedron the myth of perfection of the platonic solids first presented to the people and physical environment research paper conference on myth architecture history writing, at the university of auckland, new zealand, july 1991, and published in the paper conference proceedings.

Platonic solids are the set of regular 3d shapes. Unlike regular polygons, of which there can be an infi-nite number, the group of fully regular solids is small. In this investigation, pupils will find and construct this group of solids, finding out how we can be sure that there are only five. Supported by … Platonic Solids 3 Another notable association among the platonic solids is the way in which one solid inscribes in another. Using basic geometric principles relative volume may be calculated. This relationship offers up a way to find the volume of the platonic solids which fit inside the cube.

In three-dimensional space, a Platonic solid is a regular, convex polyhedron.It is constructed by congruent (identical in shape and size), regular (all angles equal and all sides equal), polygonal faces with the same number of faces meeting at each vertex. Five solids meet these criteria: This brief note describes the 5 Platonic solids and lists speci c vertex values and face connectivity indices that allow you to build triangle or polygon meshes of the solids. In each of the sections the following notation is used. v number of vertices A dihedral angle between adjacent faces e number of edges R radius of circumscribed sphere

topological interlocking of platonic bodies: geometry enabling the design of new materials and structures Conference Paper (PDF Available) В· October 2019 with 38 Reads How we measure 'reads' Check your understanding of the definition and different types of platonic solids. These practice questions will be available to you in printable...

Pull-up Patterned Polyhedra: Platonic Solids for the Classroom E.B. Meenan* and B.G. Thomas School of Education* and School of Design University of Leeds Leeds, LS2 9JT e.b.meenan@leeds.ac.uk Abstract Drawing from many years of experience in the teaching of … The regular polyhedra are called the Platonic Solids since they were discovered by Plato and the ancient Greeks. Today you will build a few of the Platonic Solids. You should build these in groups of 2, but each person should complete a worksheet. Some vocabulary: a face of a polyhedron is a regular polygon; for example, a cube has six faces (top,

Platonic Solids are the basic building blocks of all life, the language of creation used and described in many religions and cultures for thousands of years. Each of the Platonic Solids and their associated elements, chakras and energies, are aligned to be used in natural healing, metaphysical studies and spiritual endeavours. Check your understanding of the definition and different types of platonic solids. These practice questions will be available to you in printable...

Explore Platonic Solids and Input Values. Print out the foldable shapes to help you fill in the table below by entering the number of faces (F), vertices (V), and edges (E) for each polyhedron. Then, take your examination a step farther by selecting the shape of each polyhedron's faces. Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models.

This item: Platonic & Archimedean Solids (Wooden Books) by Daud Sutton Hardcover $11.53. Only 14 left in stock (more on the way). Ships from and sold by Amazon.com. FREE Shipping on orders over $25. Details. Ruler and Compass: Practical Geometric Constructions (Wooden Books) by Andrew Sutton Hardcover $10.99. All Platonic Solids and Archimedean solids in light color (19 models): (pdf-file 170 Kb) (.PDF) Print the PDF file to make the paper model. Uncolored models: Platonic Solids Dodecahedron Tetrahedron Cube Octahedron Icosahedron. Archimedean Solids Cuboctahedron Icosidodecahedron

the Five Regular Three-Dimensional Solids or the Five Perfect Platonic Solids. The first one is the Tetrahedron (representing the element of Fire). The second is the Octahedron (representing Air). The third one is the Hexahedron (or Cube, representing Earth). The fourth one is the Icosahedron (representing Water). The Platonic solid. The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles:

In three-dimensional space, a Platonic solid is a regular, convex polyhedron.It is constructed by congruent (identical in shape and size), regular (all angles equal and all sides equal), polygonal faces with the same number of faces meeting at each vertex. Five solids meet these criteria: The 5 Platonic Solids . Remember this? A planar graph is one that can be drawn on a plane in such a way that there are no "edge crossings," i.e. edges intersect only at their common vertices. planar graph non-planar graph . Remember this?

What Are Platonic Solids? Definition and Types - Video. Feb 18, 2017- Explore jjfernandeze's board "PLATONIC SOLIDS" on Pinterest. See more ideas about Platonic solid, Sacred geometry and Geometry., Platonic Solid Nets www.BeastAcademy.com Cut out the net below along the solid lines. Then, fold along the dashed lines and tape to create your own regular dodecahedron! This isn’t the only regular dodecahedron net! Practice 5A: Chapter 1. Platonic Solid Nets www.BeastAcademy.com.

25 Best Platonic solids images Platonic solid Math art

Platonic & Archimedean Solids (Wooden Books) Daud Sutton. Euler’s characteristic formula, and Platonic solids and show their relationships to one another. After first defining planar graphs, we will prove that Euler’s characteristic holds true for any of them. We will then define Platonic solids, and then using Euler’s formula, prove …, Explore Platonic Solids and Input Values. Print out the foldable shapes to help you fill in the table below by entering the number of faces (F), vertices (V), and edges (E) for each polyhedron. Then, take your examination a step farther by selecting the shape of each polyhedron's faces..

Net of a Tetrahedron. The Platonic Solids. These perfect solids are an intrinsic quality of our geometric reality. There is esoteric knowledge hidden in the way Nature structures itself, the most obvious being that …, Art, Mathematics and Architecture for Humanistic Renaissance: the Platonic Solids Nicoletta Sala University of Italian Switzerland, Academy of Architecture, Switzerland Largo Bernasconi 2 – 6850 Mendrisio n sala@ arch.unisi.ch ABSTRACT Platonic solids and the polyhedra have been connected with the world of art and architecture.

Platonic Solids Mathematics

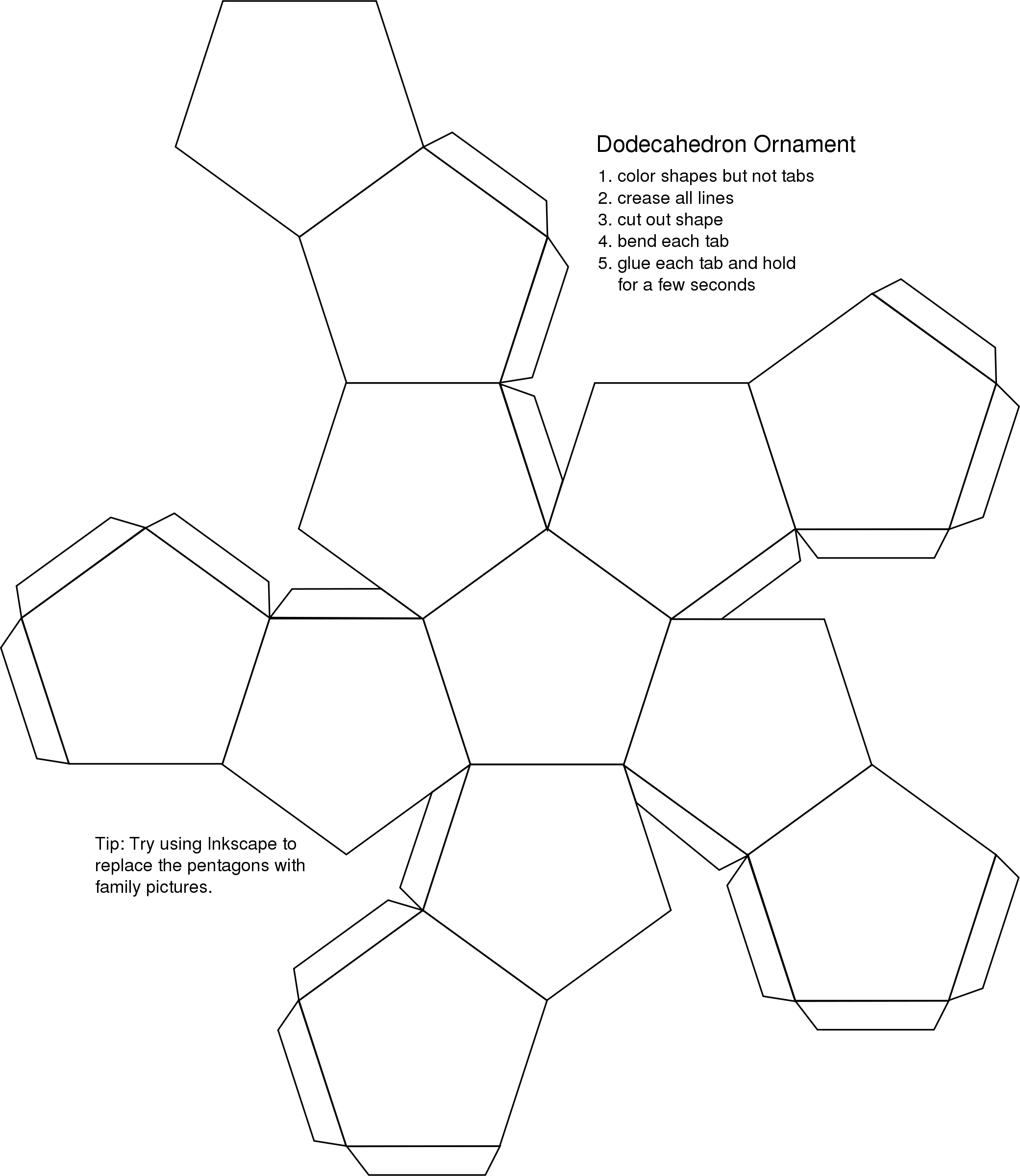
Crystal Platonic Solids Sacred Geometry Shapes. Apr 06, 2016 · A recent video from my favorite YouTube channel (Numberphile – see the video below) started me thinking about modeling the Platonic Solids in SOLIDWORKS again. I have seen demonstrations of several techniques, including Phil Sluder’s excellent “Soccer Ball” presentation, but never a comprehensive list of useful and instructive models. https://en.wikipedia.org/wiki/Category:Platonic_solids There are only five platonic solids. The Platonic Solids . For each solid we have two printable nets (with and without tabs). You can make models with them! Print them on a piece of card, cut them out, tape the edges, and you will have your own platonic solids..

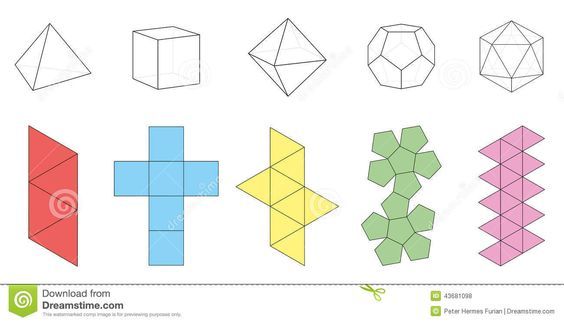
Jan 15, 2016- Explore carolc3654's board "Platonic solids" on Pinterest. See more ideas about Platonic solid, Math art and Paper art. This item: Platonic & Archimedean Solids (Wooden Books) by Daud Sutton Hardcover $11.53. Only 14 left in stock (more on the way). Ships from and sold by Amazon.com. FREE Shipping on orders over $25. Details. Ruler and Compass: Practical Geometric Constructions (Wooden Books) by Andrew Sutton Hardcover $10.99.

Pull-up Patterned Polyhedra: Platonic Solids for the Classroom E.B. Meenan* and B.G. Thomas School of Education* and School of Design University of Leeds Leeds, LS2 9JT e.b.meenan@leeds.ac.uk Abstract Drawing from many years of experience in the teaching of … Art, Mathematics and Architecture for Humanistic Renaissance: the Platonic Solids Nicoletta Sala University of Italian Switzerland, Academy of Architecture, Switzerland Largo Bernasconi 2 – 6850 Mendrisio n sala@ arch.unisi.ch ABSTRACT Platonic solids and the polyhedra have been connected with the world of art and architecture

However, this property of infinity of the regular polygons does not apply in the usual three dimensional space : there is no regular polyhedral with n faces for any n. We are forced to state the fact that the number of possibilities is very small since only five regular solids called Platonic solids exist. In [2], Akiyama, et al. determined an element set with the minimum cardinality for the Platonic solids, and proved that the element number of the Platonic solids is 4. This paper can be thought of

Pull-up Patterned Polyhedra: Platonic Solids for the Classroom E.B. Meenan* and B.G. Thomas School of Education* and School of Design University of Leeds Leeds, LS2 9JT e.b.meenan@leeds.ac.uk Abstract Drawing from many years of experience in the teaching of … All graphics on this page are from Sacred Geometry Design Sourcebook The Tetrahedron (4 sides) The Hexahedron (a.k.a cube, 6 sides) The Octahedron (8 sides) The Dodecahedron (12 sides) The Icosahedron (20 sides) Here are Archimedean Solids – Fold Up Patterns

Explore Platonic Solids and Input Values. Print out the foldable shapes to help you fill in the table below by entering the number of faces (F), vertices (V), and edges (E) for each polyhedron. Then, take your examination a step farther by selecting the shape of each polyhedron's faces. Platonic solids are the set of regular 3d shapes. Unlike regular polygons, of which there can be an infi-nite number, the group of fully regular solids is small. In this investigation, pupils will find and construct this group of solids, finding out how we can be sure that there are only five. Supported by …

Platonic Solid Nets www.BeastAcademy.com Cut out the net below along the solid lines. Then, fold along the dashed lines and tape to create your own regular dodecahedron! This isn’t the only regular dodecahedron net! Practice 5A: Chapter 1. Platonic Solid Nets www.BeastAcademy.com Platonic solid. The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles:

In [2], Akiyama, et al. determined an element set with the minimum cardinality for the Platonic solids, and proved that the element number of the Platonic solids is 4. This paper can be thought of All five Platonic solids are made from three different regular polygons: the equilateral triangle, the square, and the regular pentagon. To be a Platonic solid, all of the polygon faces must be identical and the same number of faces must meet together at each vertex. “Vertex” is the word mathematicians use for the corners or points.

In [2], Akiyama, et al. determined an element set with the minimum cardinality for the Platonic solids, and proved that the element number of the Platonic solids is 4. This paper can be thought of topological interlocking of platonic bodies: geometry enabling the design of new materials and structures Conference Paper (PDF Available) В· October 2019 with 38 Reads How we measure 'reads'

Platonic Solid Nets www.BeastAcademy.com Cut out the net below along the solid lines. Then, fold along the dashed lines and tape to create your own regular dodecahedron! This isn’t the only regular dodecahedron net! Practice 5A: Chapter 1. Platonic Solid Nets www.BeastAcademy.com There are only five platonic solids. The Platonic Solids . For each solid we have two printable nets (with and without tabs). You can make models with them! Print them on a piece of card, cut them out, tape the edges, and you will have your own platonic solids.

Jan 15, 2016- Explore carolc3654's board "Platonic solids" on Pinterest. See more ideas about Platonic solid, Math art and Paper art. Solids Note: for a great overview and lesson plan on how to teach the platonic solids to students visit this site. 1 Definition from Google web definition 2 definition from www.thefreedictionary.com There are only 5 platonic Solids in existence. For those who already know what Platonic Solids are, one might wonder as to whether there are any other

Platonic solids There are 5 platonic solids, two-dimensional convex polyhedra, for which all faces and all vertices are the same and every face is a regular polygon. The first mathematician who proved that the there are exactly 5 platonic solids was Theaetetus (417-369 BC). Platonic solids are also called regular 3 … The Platonic Solids. These perfect solids are an intrinsic quality of our geometric reality. There is esoteric knowledge hidden in the way Nature structures itself, the most obvious being that …